CÁLCULO INTERATIVO
Antiderivação: a integral indefinida
Uma função F(x) é chamada de antiderivada de f(x) se:
F'(x) = f(x)
para qualquer x no domínio de f(x). O processo de obter antiderivadas é chamado de antiderivação ou integração indefinida.
Exemplo:
Mostre que F(x) = x³/3 + 5x + 2 é uma antiderivada da função f(x) = x² + 5:
d (x³/3 + 5x + 2) / dx = 3 x²⁻¹/ 3+ 5 x¹⁻¹ = x² + 5 = f(x)
Propriedade Fundamental das Antiderivadas:
Se F(x)é uma antiderivada de uma função contínua f(x), qualquer outra antiderivada de f(x)tem a forma
G(x)=F(x)+C, onde C é uma constante.
Integração indefinida
Se F(x)é uma antiderivada da função contínua f(x), todas as antiderivadas de f(x) têm a forma F(x)+C, onde C é uma constante. Vamos representar a família das antiderivadas de f(x) usando o símbolo:
∫ f(x) d x = F(x) + C
que é chamado de integral indefinida de f(x). A integral é “indefinida” porque envolve uma constante C que pode assumir qualquer valor.
Na integral ∫ f(x) dx = F(x) + C, o símbolo ∫ é chamado de sinal de integração, a função f(x) é chamada de integrando, C é a constante de integração, e dx é uma diferencial usada para indicar que x é a variável de integração.
Para qualquer função derivável F,
∫ F'(x) d x = F(x) + C
já que, por definição, F(x) é uma antiderivada de F’(x). Esta igualdade também pode ser escrita na forma:
∫ d F/d x d x = F(x) + C.
Essa propriedade das integrais indefinidas é especialmente útil em problemas aplicados nos quais é conhecida uma taxa de variações F’(x) e estamos interessados em determinados F(x).
Observação: A integração pode ser verificada a partir da derivação. Se F'(x) = f(x), a integração ∫ f(x) d x = F(x) + C está correta; se F'(x) ≠ f(x), houve algum erro no cálculo.
A ligação entre derivação e antiderivação permite obter regras para integrar a partir de regras de derivação já conhecidas.
Regras para integrar funções comuns
-
Regra da constante: ∫ k d x = kx + C, para k constante;
-
Regra da potência: ∫ xⁿ d x = (xⁿ⁺¹/ n+1) + C, para qualquer n ≠ −1;
-
Regra do logaritmo: ∫ 1/x d x =ln|x| + C, para qualquer x ≠ 0;
-
Regra da exponencial: ∫ e ᵏˣ d x = (e ᵏˣ/k) + C, para qualquer k constante ≠ 0.
Exemplos:
i) ∫ 3 d x
ii) ∫ x¹⁷ d x
iii) ∫ 1 / √(x) d x
iv) ∫ e ⁻³ˣ d x
Regras algébricas para integração indefinida
-
Regra da multiplicação por uma constante: ∫ k f(x) dx = k ∫ f(x) d x , para k constante;
-
Regra da soma: ∫ [ f(x) + g(x)] d x = ∫ [ f(x) ] d x + ∫ [ g(x) ] d x;
-
Regra da diferença: ∫ [ f(x) − g(x)] d x = ∫ [ f(x) ] d x − ∫ [ g(x) ] d x.
Exemplos:
i) ∫ (3x⁵ + 8x³ − 3x² + 5) d x
ii) ∫ ((x³ + 2x − 7) / x) d x
iii) ∫ (3 e⁻⁵ᵗ + √(t)) d x




Problemas práticos de valor inicial:
Equação diferencial é qualquer equação que envolve uma ou mais derivadas. As equações diferencias são usadas em modelagem e aparecem em muitas aplicações práticas do cálculo. Problema de valor inicial é um problema que envolve a solução de uma equação diferencial com uma condição inicial específica.
Exemplos:
1) A população P(t) de uma colônia de bactérias t horas depois de iniciada uma observações está variando a uma taxa dada por
dP / dt = 200 e ⁰,¹ᵗ + 150 e ⁻ ⁰,⁰³ᵗ
Se a população era de 200000 bactérias quando a observações começaram, qual será a população 12
horas mais tarde?
2) Um carro está se movendo em uma estrada plana e retilínea a uma velocidade de 65 quilômetros por hora (18 metros por segundo) quando o motorista tem que frear para evitar um acidente. Se os freios fazem com que o carro perca velocidade à taxa de 6 metros por segundo ao quadrado, que distância o carro percorre até parar?
Integração por substituição
Muitas integrais podem exigir o uso de métodos e artifícios apropriados. Um amplamente utilizado é o método da mudança de variável, chamado de integração por substituição (o inverso da regra da cadeia na derivação).
-
Escolha uma substituição u = u(x) que "simplifique"o integrando f(x). Algumas dicas u(x) estratégico para o cálculo:
-
Se possível, escolha u de tal forma que u'(x) seja parte do integrando f(x);
-
Procure escolher u como a parte do integrando que torna a função f(x) difícil de integrar diretamente, como um radicando, um denominador ou um expoente;
-
Não exagere em substituições;
-
Não desista. Se a substituição que você experimentou não resultar em uma integral fácil de resolver, use uma substituição diferente;
-
Tendo u(x) bem estabelecido, segue-se para os próximos passos:
-
-
Expresse toda a integral em termos de u e d u = u'(x) d x. Isto significa que todos os termos que envolvem x e d x devem ser transformador em termos que envolvem u e d u;
-
Depois de executado o passo 2, a integral deve estar na forma ∫ f(x) d x = ∫ g(u) d u. Se possível, calcule o valor desta integral transformada determinando uma antiderivada G(u) e g(u);
-
Substitua u por u(x) em G(u) para obter uma antiderivada G(u(x)) para f(x) de modo que
∫ f(x) d x = G(u(x)) + C,
oferecendo o resultado de acordo com a variável inicial de integração.
Exemplos:
i) ∫ √(2x + 7) d x
ii) ∫ 8x (4x² − 3)⁵ d x
iii) ∫ (x³)(eˣ⁴⁺²) d x
iv) ∫ (x / (x−1)) d x
v) ∫ [(3x + 6) / √(2x³ + 8x + 3)] d x
Observe: ∫ (x⁴)(eˣ²⁺²) d x







Integração definida e
Teorema Fundamental do Cálculo
Área sob uma curva
A área sob uma curva pode ser expressa como o limite de uma soma que recebe o nome de integral definida. Observe:
Considere a área da região sob a curva y = f(x) em um intervalo a ≤ x ≤ b, onde f(x) ≥ 0 e f é contínua, como mostra a figura:

Quando estiver diante de um problema desconhecido, procure relacioná-lo a um problema conhecido.
Neste caso em particular, podemos não saber como calcular a área sob a curva dada, mas sabemos como calcular a área de um retângulo. Assim, dividimos a região em uma série de regiões retangulares e calculamos o valor aproximado da área A sob a curva y = f(x) somando as áreas dessas regiões retangulares.
Para começar, divide-se o intervalo a ≤ x ≤ b em n subintervalos iguais de largura ∆x = (b−a)/n retângulos, tais que o retângulo de ordem j tenha uma largura igual a ∆x e uma altura a f(x). O processo está ilustrado na figura:
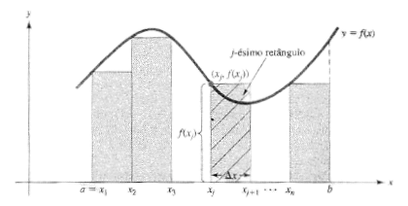
A área do retângulo de ordem j, f(xⱼ)∆x, é aproximadamente igual à área sob a curva no intervalo xⱼ≤x≤xⱼ₊₁. A soma das áreas do n retângulos é:
Sₙ = f(x₁)∆x + f(x₂)∆x + ... + f(xₙ)∆x = [ f(x₁) + f(x₂) + ... + f(xₙ)]∆x
que é aproximadamente igual à área total A sob a curva.

Note: Quanto maior o número de intervalos, melhor a aproximação.
Assim, pode-se definir para uma área A sob uma curva f(x):
Seja f(x) ≥ 0 no intervalo a ≤ x ≤ b. A área sob a curva y = f(x) no intervalo a ≤ x ≤ b é dada por
A = lim [ f(x₁) + f(x₂) + ... + f(xₙ)]∆x
onde xⱼ é a extremidade esquerda do subintervalo de ordem j se o intervalo a ≤ x ≤ b for dividido em n partes iguais de comprimento ∆x = (b−a) / n.
Exemplo:
Seja R a região sob a curva da função f(x) = 2x + 1 no intervalo 1 ≤ x ≤ 3. Calcule a área da região R como o limite de sua soma.
n→+∞
Integração definida
Seja f(x) uma função contínua no intervalo a ≤ x ≤ b. Suponha que este intervalo tenha sido dividido em n partes iguais de largura ∆x = (b−a)/n e seja xₖ um número pertencente ao intervalo de ordem k, para k =1, 2, ..., n. Forma-se a soma
[ f(x₁) + f(x₂) + ... + f(xₙ) ]∆x
conhecida como Soma de Riemann.
Nesse caso, a integral definida de f(x) no intervalo a ≤ x ≤ b, representada pelo símbolo ∫ f(x) d x, é dada pelo limite da soma de Riemann quando n→∞, ou seja:
∫ f(x) d x = lim [ f(x₁) + f(x₂) + ... + f(xₙ) ]∆x
A função f(x) recebe o nome de integrando e os números a e b são chamados de limite inferior de integração e limite superior de integração, respectivamente. O processo de calcular uma integral definida é chamado de integração definida.
n→+∞
a
b
b
a
b
a
Área como uma integral definida
Se f(x) é uma função contínua e f(x) ≥ 0 no intervalo a ≤ x ≤ b, a área A da região R sob a curva y= f(x) no intervalo a ≤ x ≤ b é dada pela integral definida A =∫ f(x) d x.
Teorema fundamental do Cálculo
Se a função f(x) é contínua no intervalo a ≤ x ≤ b.
∫ f(x) d x = F (b) − F(a)
onde F(x) é a antiderivada de f(x) no intervalo a ≤ x ≤ b.
a
b
Regras para integrais definidas
As regras a seguir podem ser usadas para facilitar o cálculo de integrais definidas.
Sejam f e g funções contínuas no intervalo a ≤ x ≤ b. Nesse caso,
-
Regra da multiplicação por uma constante: ∫ kf(x) d x = k ∫ f(x) d x, onde k é uma constante.
-
Regra da soma: ∫ [f(x) + g(x)] d x = ∫ [f(x)] d x + ∫ [g(x)] d x
-
Regra da diferença: ∫ [f(x) − g(x)] d x = ∫ [f(x)] d x − ∫ [g(x)] d x
-
Quando limite superior = limite inferior de integração: ∫ f(x) d x = 0
-
∫ f(x) d x = − ∫ f(x) d x
-
Regra da subdivisão: ∫ f(x) d x = ∫ f(x) d x + ∫ f(x) d x , para a < c < b
b
b
b
b
b
b
b
b
b
b
b
a
a
a
a
a
a
a
a
a
a
a
c
c
b
b
a
b
Exemplos:
i) ∫ [(1/x) − x²]d x
4
1
ii) ∫ (e⁻ˣ + √x) d x
1
0
iii) ∫ 8x (x² + 1)³ d x
1
0
iv) ∫ ln/x d x
2
¼





Aplicações das integrais definidas
Método para usar a integração definida em problemas práticos
Para “acumular” uma grandeza Q em um intervalo a ≤ x ≤ b através da integração definida, fazemos o
seguinte:
-
Dividimos o intervalo a ≤ x ≤ b em n subintervalos iguais de largura ∆x =(b−a)/n. Escolhemos um
número xⱼ no subintervalo j para j = 1, 2, ..., n; -
Supomos que a contribuição do subintervalo j para o valor total da grandeza Q é dada, aproximadamente, pelo produto f(xⱼ)∆x, onde f(x) é uma função apropriada que seja contínua no intervalo a ≤ x ≤ b;
-
Somamos as contribuições de todos os subintervalos para estimar o valor total da grandeza Q
através da soma de Riemann [ f(x₁) + f(x₂) + ... + f(xₙ) ]∆x; -
Tornamos exata a aproximação do 3o passo calculando o limite da soma de Riemann quando n→∞ para expressar Q na forma de uma integral definida: Q = lim [ f(x₁) + f(x₂) + ... + f(xₙ) ]∆x = ∫ f(x) dx;
-
Usamos o teorema fundamental do cálculo para calcular ∫ f(x) dx, desta forma, obter o valor desejado de Q.
Área entre duas curvas
Em certos problemas práticos, pode ser interessante representar uma grandeza de interesse na forma da área entre duas curvas. Inicialmente, vamos supor que f e g são funções contínuas e não negativas (ou seja, que f(x) ≥ 0) e que satisfazem a desigualdade f(x) ≥ g(x) no intervalo a ≤ x ≤ b, como mostra a
figura.

a
b
Resumindo: se f(x) e g(x) são funções contínuas, com f(x) ≥ g(x) no intervalo a ≤ x ≤ b, a área A entre as curvas y = f(x) e y = g(x) no intervalo é dada por:
A = ∫ [f(x) − g(x)] d x
Exemplos:
i) Determine a área da região R limitada pelas curvas y = x³ e y = x².
ii) Determine a área da região limitada pela reta y = 4x e pela curva y = x³ +3x².
Variação total
Se Q’(x) é contínua no intervalo a ≤ x ≤ b, a variação total de Q(x) quando x varia de x = a até x = b é dada por:
Q(b) − Q(a) = ∫ Q'(x) d x
a
b
Exemplo:
Uma amostra de proteína de massa m (em gramas) se decompõe em aminoácidos a uma taxa dada por: dm/dt = - 30/ (t+3)² , em gramas/horas. Qual é a variação total de massa da amostra de proteína durante as primeiras 2 horas?
Valor médio de uma função
Como segunda ilustração do uso da integral definida em problemas práticos, vamos calcular o valor médio de uma função, que é de interesse em várias situações.
Seja f(x) uma função contínua no intervalo a ≤ x ≤ b é dado pela integral definida
V = [1/(b − a)] ∫ f(x) d x
a
b
Exemplo:
Um pesquisador modela a temperatura T (em °C) em uma certa cidade canadense entre as 6 e as 18 h
usando a função
T(t) = 3 − 1/3 (t − 4)² para 0 ≤ x ≤ 12
onde t é o número de horas após 6 h.
a) Qual é a temperatura média da cidade durante o horário comercial, das 8 às 17 h?
b) Em que instante (ou instantes), durante o horário comercial, a temperatura é igual à temperatura média calculada no item (a)?
Interpretação do Valor médio como uma taxa
O valor médio de uma função f(x) em um intervalo a ≤ x ≤ b no qual f(x) é contínua é igual à taxa média de variação de qualquer antiderivada F(x) de f(x) no mesmo intervalo.
Interpretação geométrica do Valor médio
O valor médio de f(x) em um intervalo a ≤ x ≤ b no qual f(x) é continua e satisfaz à desigualdade f(x) ≥ 0 é igual à altura de um retângulo cuja base é o intervalo e cuja a área é igual à área sob a curva y = f(x) no intervalo a ≤ x ≤ b.
Volume de um sólido de revolução
A técnica consiste em expressar o volume do sólido como o limite de uma soma de volumes de discos. Suponha que S seja o sólido formado pela rotação em torno do eixo x da região R sob a curva y = f(x) entre os pontos x = a e x = b, como mostra a figura. Dividindo o intervalo a ≤ x ≤ b em n subintervalos iguais de largura ∆x, pode-se aproximar a região R por n retângulos em torno do eixo x.


a
b
O volume aproximado do sólido S é dado pela soma dos volumes de vários discos. Como o j-ésimo disco cilíndrico tem raio rⱼ = f (xⱼ) e espessura ∆x, o volume do disco é:
Volume do j-ésimo disco = (área da seção reta circular)(largura) = πrⱼ² (largura) = π [f(xⱼ)]² ∆x. O volume total de S é aproximadamente igual à soma dos volumes dos n discos, ou seja,
Volume de S ≈ ∑ⁿⱼ₌₁ π [f(xⱼ)]² ∆x
A aproximação tende para o valor exato quando n tende a infinito e
Volume de S = lim n→+∞ π [f(xⱼ)]² ∆x = π ∫ [f(x)]² d x
Em resumo, suponha que f(x) é contínua e f(x) ≥ 0 no intervalo a ≤ x ≤ b e seja R a região sob a curva y =
f(x) entre x = a e x = b. Nesse caso, o volume do sólido S formado pela rotação de R em torno do eixo x é
dado por
Volume de S = π ∫ [f(x)]² d x
a
b
Exemplos:
i) Determine o volume do sólido S formado pela rotação em torno do eixo x da região sob a curva y = x² +1entre x = 0 e x = 2.
ii) Um tumor tem aproximadamente a mesma forma que o sólido formado pela rotação da região sob a curva y = ⅓ √(16 − x²) em torno do eixo x, onde x e y estão em centímetros. Determine o volume do tumor.
Outros tópicos de integração
Integração por partes
A integração por partes é uma técnia de integração baseada na regra do poduto para derivadas. Em particular se u(x) e v(x) são funções deriváveis de x, temos:
d [u(x) v(x)] = u(x) d v + v(x) d u
d x d x d x
e, portanto,
u(x) d v / d x = d [u(x) v(x)] / d x − v(x) d u / d x
Integrando ambos os membros desta equação em relação a x, obtemos:
∫ [u(x) d v / d x] d x = ∫ [d [u(x) v(x)] / d x] d x − ∫ [v(x) d u / d x] d x
∫ [u(x) d v / d x] d x = u(x) v(x) − ∫ [v(x) d u / d x] d x
já que u(x)v(x) é uma antiderivada de d [u(x) v(x)] / d x.
Como d v = (d v/ d x) d x e d u = (d u/ d x) d x, podemos escrever esta expressão na forma mais compacta
∫ u d v = u v − ∫ v d u
Essa expressão é chamada de fórmula de integração por partes. A grande vantagem desta fórmula é que, se uma integral da forma ∫ f(x) d x puder ser expressa na forma ∫ u d v, onde u e v são funções
de x, ∫ f(x) d x = ∫ u d v = u v − ∫ v d u, e a integral que queremos resolver poderá ser substituída diretamente por ∫ v d u. Se ∫ v d u for mais fácil de calcular que ∫ u d v, a substituição facilitará o cálculo de ∫ f(x) d x.
Método para usar a integração por partes
Para determinar uma integral ∫ f(x) d x usando a fórmula de integração por partes:
-
Tendo a função f(x), estabeleça u e v tais que f(x) d x = u d v. Procure escolher um u para o qual d u seja mais simples que u, e um d v que seja fácil de integrar;
-
Organizar os cálculos de d u e v da seguinte forma: define u, encontra d u isolando-o a partir do cálcuclo de de d u/d x; define d v, encontra v calculando ∫ d v;
-
Complete a integração calculando ∫ v d u. O resultado é:∫ f(x) d x = ∫ u d v = u v − ∫ v d u;
-
Acrescente “+ C” apena quando terminar os cálculos.
Exemplos:
i) ∫ (x²)ln(x)d x
ii) ∫ (x)(e²ˣ) d x
iii) ∫ (x)(√(x + 5) d x
iv) ∫ ln(x) d x
v) ∫ (x²)(e²ˣ) d x





Tabela de integrais
A maioria das integrais encontradas nas ciências sociais, econômicas e biológicas pode ser calculada
usando as expressões básicas de integral indefinida/definida e os métodos de substituição e integração por partes. Porém, às vezes, aparecem integrais que não podem ser calculadas por essas soluções. Algumas, de fato, não possuem solução analítica; outras são encontradas em tabelas de integrais.
Desse modo, a resolução pode ser feita consultando uma tabela. As principais estão abaixo:




Exemplos:
i) ∫ 1 / ((x)(3x − 6)) d x
ii) ∫ 1 / (6 − 3x²) d x
iii) ∫ 1 / (√(4x² − 9)) d x
iv) ∫ (x³)(eˣ⁵) d x





+∞
a
Integrais impróprias
A integral imprópria de f(x) no intervalo infinito x ≥ a é representada por ∫ f(x) d x.
Se f(x) é uma função contínua para x ≥ a :
∫ f(x) d x = lim ∫ f(x) d x
Quando o limite que define a integral imprópria existe, dizemos que a integral converge; quando o limite não existe, dizemos que a integral diverge.
+∞
+∞
a
a
n→+∞
Exemplos:
i) ∫ 1 / (x²) d x
+∞
1
ii) ∫ 1 / (x) d x
+∞
1